Transformaciones Geométrica



CONCEPTOS
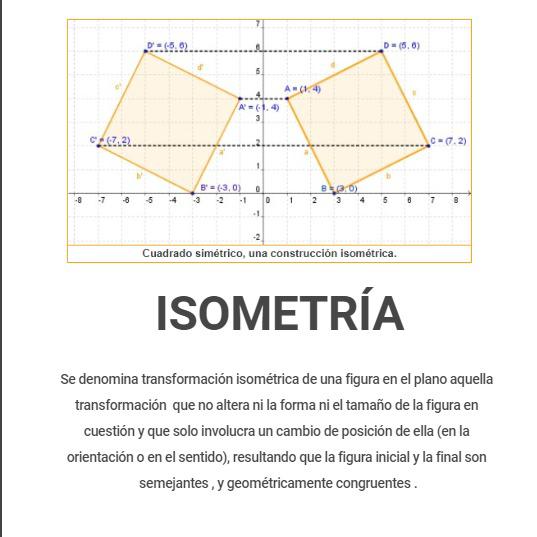
- Isometría
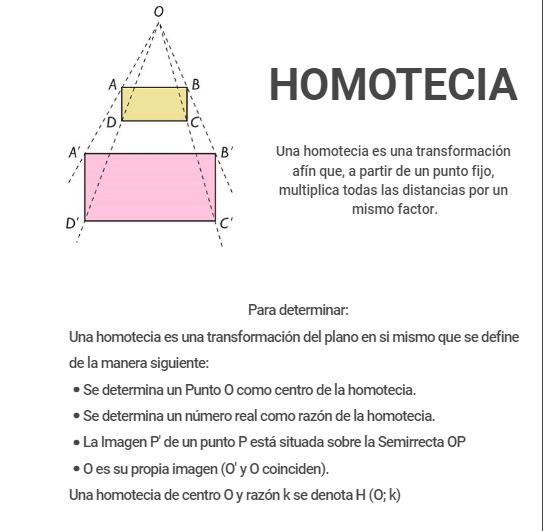
- Concepto de homotecia de un punto
- Regla para determinar homotecias en el plano
- Concepto de semejanza (como transformación geométrica)
- Regla para determinar semejanzas en el plano
PROCEDIMIENTOS
- Identificación transformaciones geométricas.
- Clasificación de las trasformaciones geométricas
- Construcción de homotecia de una figura respecto a una constante.
- Construcción de semejanza de una figura en el plano.
- Modelación de las transformaciones geométricas.
ACTITUDES Y VALORES
- Aprecio por el uso de las transformaciones geométricas.
- Interés en aplicaciones de las transformaciones geométricas que se encuentran en su entorno.
- Disfrute al modelar situaciones de su entorno a través de las transformaciones geométricas.
RECORDATORIO DE LA UNIDAD II
Bienvenidos a "Magic Unit", como su nombre lo dice una unidad mágica. Aquí podrás encontrar todo lo relacionado a las transformaciones geométricas, como su descubrimientos han cambiado al mundo y como podemos relacionarlos con nuestro entorno diario. El desarrollo de esta unidad está basado como tipo juego, donde mientras mas actividades realices, mas cerca estarás de la meta.
Pero antes.... favor de leer la siguiente frase.



Antes de iniciar el juego es bueno que observes la SUPER interesante historia de las transformaciones geométricas. Te ayudará mucho, créeme.
CONOCE TUS FORTALEZAS Y DEBILIDADES
Cuando inicias un nuevo proyecto siempre es bueno saber que tanto conoces acerca del mismo, por esta razón me gustaría que le des clic al siguiente link donde entrarás a una pagina llamada "Cerebriti" el cual es una plataforma de juegos virtuales y donde a la vez conocerás que tanto sabes sobre el tema de las transformaciones geométricas.

PRIMER NIVEL
OBTEN VENTAJAS DE TUS OPONENTES
Es claro que antes de iniciar un juego debes conocer de que se trata y cuales son tus oponentes mas hábiles. Pero no te preocupes, estamos aquí para ayudarte. Para llegar al nivel deseado primero debes conocer los conceptos básicos respeto a las transformaciones geométricas.
Para esto te invito a investigar acerca de que es la isometría, conceptos de homotecia de un punto, las reglas para determinar homotecias en el plano, concepto de semejanza respecto a las transformaciones geométricas y por último las reglas para determinar semejanzas en el plano. Luego de investigarlos realiza un infogram donde podrás recopilar todos los datos que investigaste y nunca se te olvidarán.
Para realizar el infogram puede auxiliarte de las siguientes plataformas:
- https://www.canva.com/
- https://infogram.com/
- https://www.canva.com/
- https://infogram.com/
Resultados de los alumnos

FELICIDADES, TU ESFUERZO ES NOTABLE. PERO ANTES DE CONTINUAR AL SIGUIENTE NIVEL NOS GUSTARÍA QUE REALICES ESTE PEQUEÑO EJERCICIO PARA GARANTIZAR SI DOMINAS LOS CONCEPTOS INVESTIGADOS Y LOS PUEDES RELACIONAR CON LA VIDA.

VISTE QUE FÁCIL FUE.

SEGUNDO NIVEL
- ¿Sabías que?
- Uno de los primeros objetos que se pueden apreciar durante la historia y
que funciona con homotecia es la lupa, la cual fue creado por el filósofo Roger Bacon.
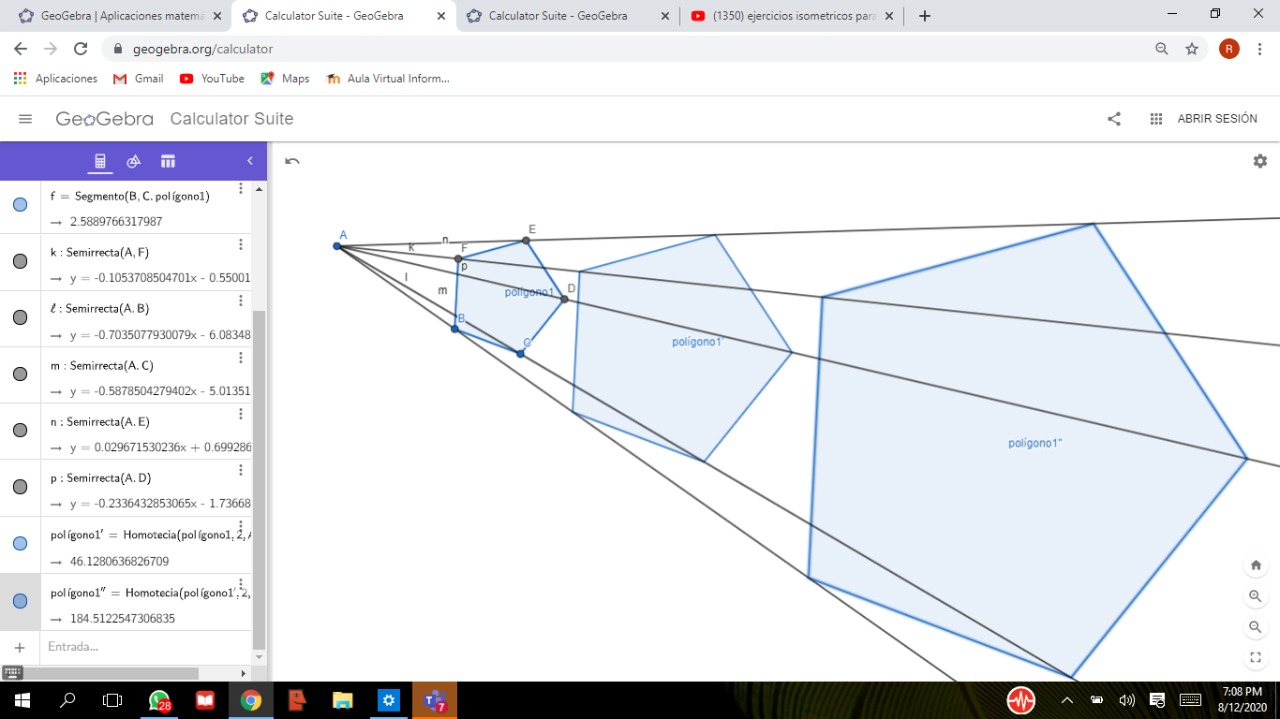
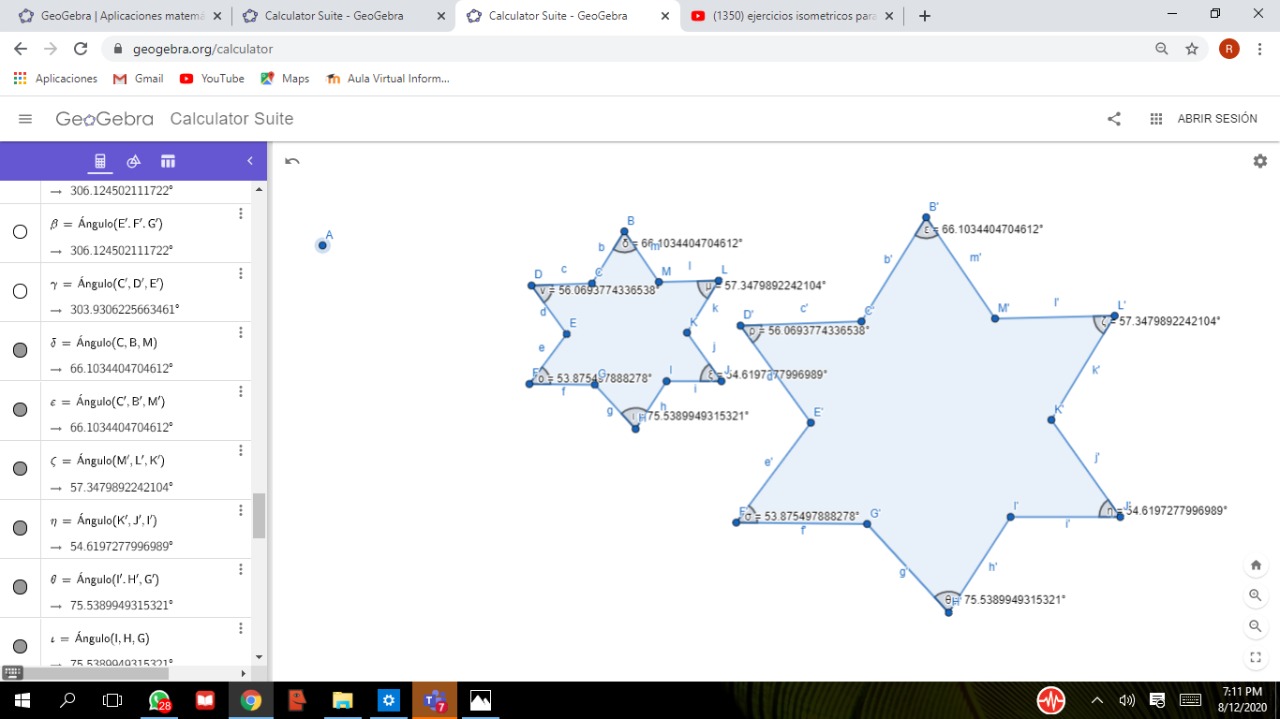
Muy buen trabajo amigo mio, creo que ya estas listo para la batalla y se que puedes lograrlo. Por lo tanto te invito a construir una homotecia de una figura respecto a una constante utilizando geogebra.
Resultados de los alumnos


- ¿Sabías que?
En el cinematografía se aplica una homotecia directa donde el punto inicial seria la lámpara de luz, el polígono original la cinta y el polígono semejante la imagen proyectada en el telón. Lo mismo pasa cuando hacemos dibujos de sombras en la pared con nuestras manos.
TERCER NIVEL
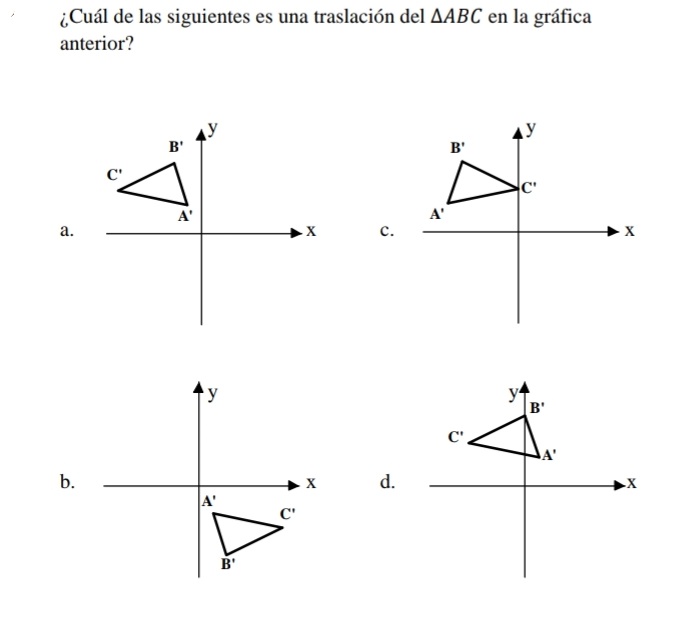
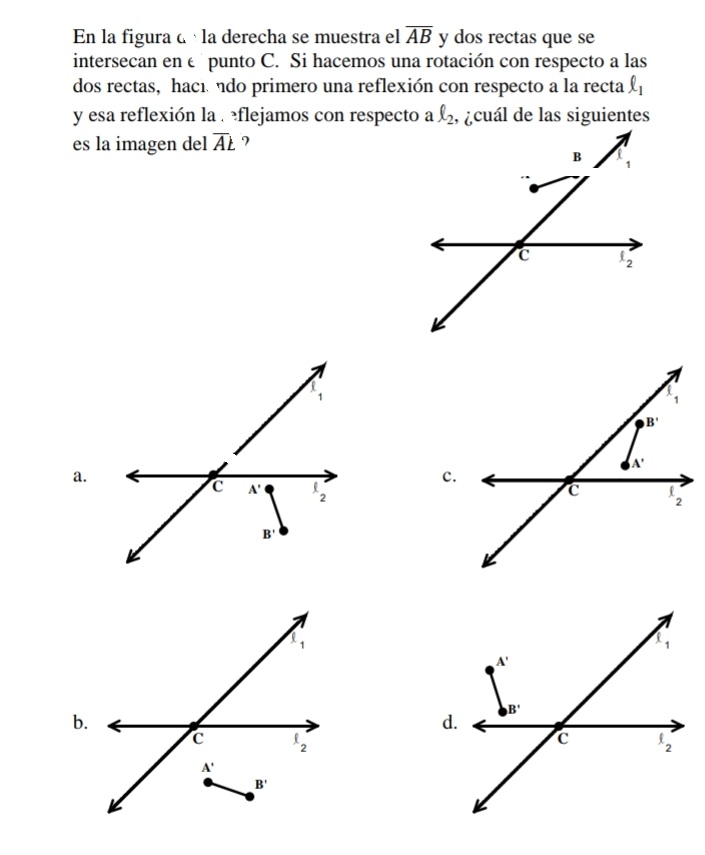
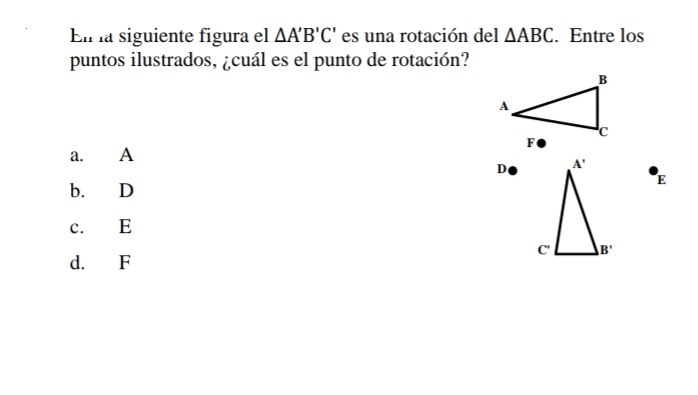
No podemos evitar lo feliz que nos sentimos de tu progreso, sin embargo ahora debes de resolver las siguientes problemáticas acerca de traslaciones y rotaciones geométricas provenientes del libro de "Transformaciones Geométricas en el plano" del Prof. Mariano Martes Pagán, luego debes grabar un vídeo con Flipgrid resolviéndolos y subir el vídeo a YouTube.
Enlaces de tutoriales que te pueden servir de ayuda:
- https://www.youtube.com/watch?v=OFt_lQYN6PI
- https://www.youtube.com/watch?v=YmxlNbzu_Yc
CUARTO NIVEL

Para realizar tu experiencia aun mas interesante nos gustaría ilustrarte como trabajan los transformaciones geométricas en esta maravillosa plataforma llamada Mozaik, donde puedes juegas y construir en 3D. En caso de no tener una cuenta aun, aquí tienes un tutorial de como realizarla.
-Transformaciones geométricas - reflexión
https://us.mozaweb.com/es/Extra-Escenas_3D-Transformaciones_geometricas_reflexion-147964
-Transformaciones geométricas - traslación
https://us.mozaweb.com/es/Extra-Escenas_3D-Transformaciones_geometricas_traslacion-147963
-Transformaciones geométricas - rotación
https://us.mozaweb.com/es/Extra-Escenas_3D-Transformaciones_geometricas_rotacion-147961
-Juego de rotación 3D
https://us.mozaweb.com/es/Extra-Escenas_3D-Juego_de_rotacion_3D-208249
QUINTO NIVEL
Lo haz hecho muy bien hasta ahora, pero creo que es momento de subir un poco mas de nivel. Por lo tanto, te reto a construir un telescopio casero. Tan solo necesitas los los siguientes materiales:- Rollos de papel higiénico, tubos o botellas de plásticos.
- Cinta adhesiva
- Dos lentillas de lupas
- Silicón
- Entre otros materiales.

Resultados de los alumnos

SEXTO NIVEL

¿Sabías que?
La mayoría de los animales tienen simetría bilateral, lo que significa que se pueden dividir en dos mitades idénticas. Incluso las personas tienen simetría bilateral, y algunos científicos creen que la simetría del ser humano es el factor más importante que influye en nuestra percepción de la belleza.
Hay quienes dicen que el rostro simétrico es aquel cuyo lado izquierdo es exactamente igual al lado derecho y si trazamos una línea vertical justo por la mitad del rostro, ambos lados serían idénticos; sin embargo, otros científicos que estudian la simetría facial, no creen que el rostro deba ser idéntico en ambos lados.
Por lo tanto, en este nivel decidimos que hagas algo mas personal, no te preocupes, no donarás un riñón o algo por el estilo, al menos no aun. Pero lo que si te pediremos es lo siguiente, con la ayuda de un editor de foto o con el mismo powerpoint coge tu teléfono y tomate una selfie (sin lengua afuera por favor), luego divide tu cara de ambos lados y verifica si tienes ambos lados del rostro identifico. Esto es gracias a la simetría axial.
Resultados de los alumnos

SÉPTIMO NIVEL


Los ejercicios isométricos, en caso de que no sepas que son, son ejercicios corporales que implican una tensión muscular pero que no generan movimiento de contracción y extensión de los músculos. Si decides del reto, te presentamos los siguientes ejercicios isométricos que puedes realizar desde casa. Entre ellos están: Plancha Estática (sobre codos).

Sentadilla estática en el aire

Plancha Estática Lateral


NO HA SIDO UN TRAYECTO FÁCIL PERO SI HA SIDO MUY SATISFACTORIO, ESPERAMOS QUE HAYAS SENTIDO LOS MISMO.

Para culminar necesitamos que hagas una última actividad y es, que realices la siguiente evaluación para garantizar, que tanto aprendiste con nuestro blog. La evaluación sera quizizz solo tienes que seguir las instrucciones de la plataforma.

https://quizizz.com/join/quiz/5f35f330202485001f4d9945/start?studentShare=true


